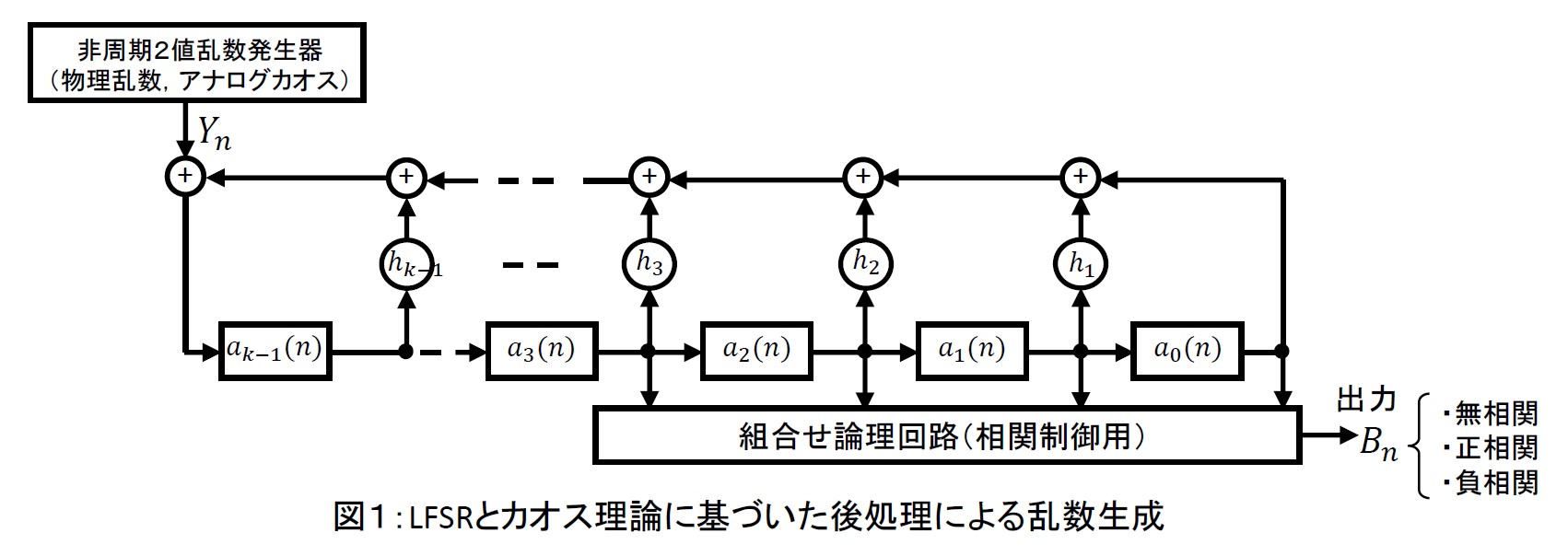
モンテカルロ法においては、用いる乱数の長さN を長くすればするほど精度が向上するが、その乱数が一旦周期に陥ると、その後は周期的な計算を繰り返すのみで、それ以上の精度向上は望めない。したがって、物理乱数のように非周期的な乱数であれば、望む精度が得られるまで、どこまでもN を長くすることができる。しかしながら、一般に物理乱数自体の統計的性質は（偏りや相関があるという意味で）あまり良くないため、後処理によって加工して用いられる。一次元写像によるカオスは、通常の擬似乱数と同様、計算機で簡単に生成できるが、有限ビット演算のため、最終的には周期的な時系列となる。カオスの本質は実数の複雑さ（すなわちアナログ性）であり、アナログ電子回路で実現すれば非周期的なカオス乱数を生成可能であるが、素子値の誤差や雑音の影響等で、所望の特性を得ることが困難である。そこで、線形／非線形フィードバックシフトレジスタ（LFSR/NFSR）による後処理により、所望の特性を得ることを検討する。LFSR/NFSR は有名なカオス写像であるベルヌイ写像の有限ビット近似とみなすことができるため、ここにカオス理論を活用することができる。本研究では、この後処理の手法を種々検討し、元の乱数（物理乱数やアナログカオス）を様々な特性（無相関、正相関、負相関）の乱数に変換することを試みる。また、生成した乱数を、モンテカルロ積分やモンテカルロシミュレーションへ適用し、その有用性を検証する。