【技術紹介】

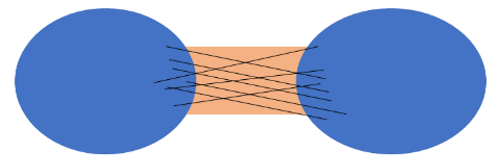
　グラフは頂点の集合とそれらを結ぶ辺からなります。中でもエクスパンダー (グラフ) とは、辺の数は少ないながらも、頂点たちをどのような2つのグループに分けても、2つのグループは一定数の割合の辺でつながる (図1) という意味で「よくつながっている」グラフを指します。エクスパンダーは整数論、群論、組合せ論などの数学でも重要である一方で、情報科学にも深く関係します。
　研究の一例として、以下の内容を紹介します。

図1

ハッシュ関数の構成・安全性解析とエクスパンダー
　(暗号学的) ハッシュ関数は、任意のテキストを固定長のビット列に変換する関数であり、一方向性や衝突困難性などの安全性条件を満たす必要があります (図2)。ハッシュ関数は暗号方式の基礎の一つであり、電子署名やメッセージ認証などの現代の情報技術に応用されます。実は、エクスパンダー上のランダムウォークを用いてハッシュ関数を構成することができ、特定の関数値の出現頻度からの情報漏洩を防止することが可能です。一方で、その安全性検証は土台となるエクスパンダーの内部構造に (極めて!) 大きく依存するため、エクスパンダーの内部構造を数学的に詳しく調べる必要があります。
　当研究室では、代数的に構成したエクスパンダーグラフに基づくハッシュ関数の構成と安全性検証を行っています。組合せ論、線形代数学、群論、整数論、離散確率論などの様々な数学を駆使しながら、現実の安全な情報技術への貢献を目指せる点が魅力の一つかもしれません。

図2

　この他にも、圧縮センシングなどのスパース復元の研究や、誤り訂正符号の構築などの情報数学の課題にもエクスパンダーを応用して取り組んでいます。