|
マジョライゼーションの理論は対称性に関連した不等式論であるが,統計数学を初め広い応用をもつ。その深化を研究する中で,非対称化,球面化した議論の展開に成功した。そのことにより,順序制約下での尤度比検定の検出力に関する未解決問題に対して数学的な解決を与えた。現在は拡張されたマジョライゼーションの幾何学的性質の解明を中心に研究している。(Figure 1)
|
|
同等性の仮説に対する検定については十分な検出力が得られないことが知られており,検出力を高めるための方法論がいろいろと論じられているが,これらは順序制約問題とも深く関連を持っている。本研究では,信頼区間の対称化を応用した検定の構成法や順序制約問題との関連性について研究している。 (Figure 2)
|
Extensions of majorization theory : Majorization is a famous theory of inequalities induced by symmetry. By asymmetrization and spherical extension of majorization theory, we gave a mathematical solution for Bartholomew’s conjectures on the power function of the LRT against order restricted alternatives. We now study geometrical properties and statistical applications of the extended majorization. (Figure 1)
Testing bioequivalece hypotheses : In bioequivalence testing problems, it is a principal problem to construct more powerful tests. We are interested in construction methods by symmetrization of confidence intervals (Figure 2). We also research the application of methodology developed in order-restricted statistical inferences to bioequivalence problems.
|
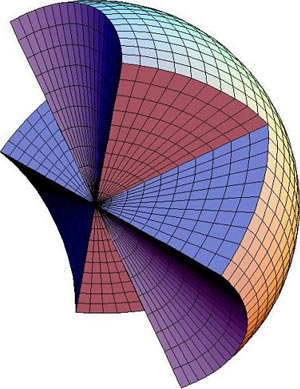
Figure 1. Image of non-convex cone defining spherical majorization |
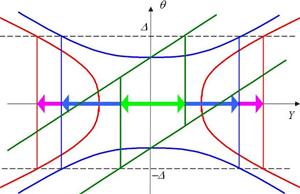
Figure 2. Symmetrization of the �shortest confidence interval
|
|