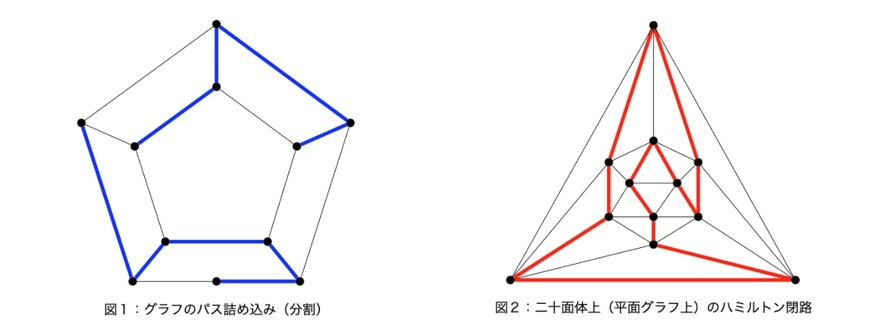
「いくつかの点」と「それらを結ぶいくつかの線」から構成される図形のことをグラフと呼ぶ（図１・２）。グラフ理論とは、与えられたグラフの構造や性質を抽象的に議論する数学の分野である。グラフは、現実社会における様々な現象を表すモデルとして用いられており、グラフ理論によってその繋がりの最適化や効率化を探ることが可能となる。実際に、通信網（インターネット）・交通網・VLSI配線などに関する多くの問題がグラフ理論上の組合せ問題として定式化される。本研究室では、下記の代表的問題を中心に、基礎研究とその応用研究を行っている。
 

• グラフの詰め込み問題とグラフの分割問題
  　グラフの詰め込み問題とは，グラフを１つの大きな箱と捉え，その箱の中に何か対象となる別のグラフをできるだけ多く入れる・詰め込む、という問題である（図１）。特に、隙間なく箱に詰め込む問題をグラフの分割問題という。対象となるグラフに応じた詰め込み・分割に対する“適切な”条件を考案し、詰め込み・分割可能性に対する“良い”指標を与える研究を行っている。また、その指標をもとに、レイアウト設計等の配置問題への応用やスケジューリング問題におけるスケジュール作成への活用法について研究を行っている。
   
• 巡回セールスマン問題とハミルトン閉路問題
  　巡回セールスマン問題とは、いくつかの地点を巡回するたくさんの経路の中から、移動コストが最小化されたものを１つ見つける、という問題であり、組合せ最適化問題の代表例の１つである。特に、移動コストを１に制限した問題がハミルトン閉路問題である。この問題に対する効率的なアルゴリズムを設計することは不可能であると考えられている。そこで、本研究室では、巡回経路（ハミルトン閉路）を効率的に探索できるグラフの特徴付けとそのグラフの構成法（図2）ならびに「グラフの詰め込み・分割問題」を利用した巡回経路の近似解法等の研究を行っている。